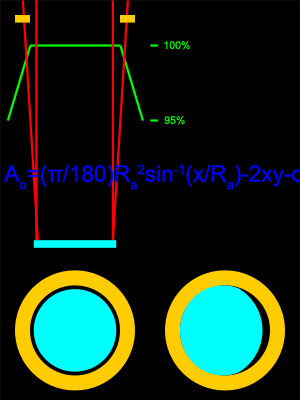
How small can the tube or secondary cage be and not start to block light from the primary mirror? The answer depends on the size of the primary, the focal length and the desired field size.
This subject is covered in a couple references but I always found the answer to be a bit simplistic. I wanted a more informative method to allow calculation of the minimal cage ring size and be able to figure the exact tradeoff I face in order to minimize the cage ring size.
The answer turned out to be a somewhat more difficult exercise that I had imagined. I could easily calculate the angles up and down the tube, these were simple trigonometry. But to come to a final answer I needed to find the area of overlap of two uneven sized circles. This took more work and a bit more geometry than I remembered and some reading in the old college textbooks was required. But there is indeed an answer, and when I used the resulting formulas to develop a spreadsheet the answers are indeed correct!
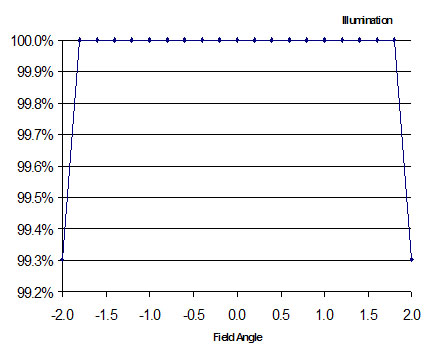
Analysis of my 6" RFT Primero. The focal length of this scope is 777mm, and it is housed in a 8" piece of aluminum irrigation tubing. The distance from the front of the primary to the front of the tube is 31.5".
I was somewhat concerned because this scope is capable of over a 3° field of view with my 35mm Panoptic eyepiece. The results show that there is no obscuration across a 3° field.
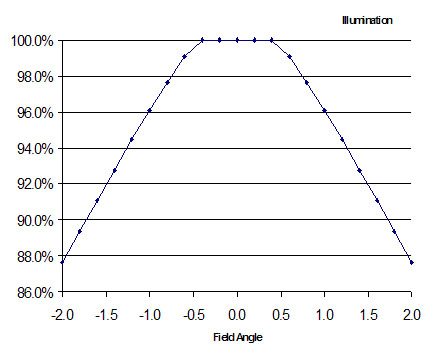
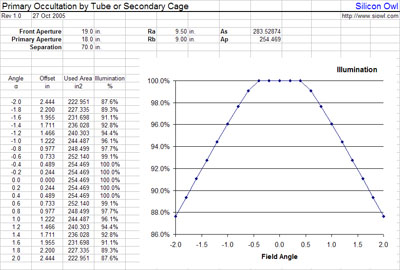
Analysis of my 18" Deep Violet. This telescope is a 18" scope with a 19" I.D. ring located 70" in front of the primary mirror.
The result is a little more interesting showing that the telescope is good for about 1° field of view at best before suffering some roll off. That is fine, as the lowest power, widest field eyepiece I have (35mm Panoptic) results in almost exactly a 1° field.
If I had some hypothetical eyepiece that resulted in a 3° field there would be almost a 10% roll off in brightness, probably objectionable.
Using the Spreadsheet
- Download the Excel spreadsheet and save to your local computer.
- Enter the ID of the upper cage ring or the ID of the optical tube.
- Enter the size of the primary mirror
- Enter the distance from the front of the primary to the front of the tube or cage ring.